Math'φsics

Menu
  • Acceuil
  • Maths
  • Physique
    • Maths
    • Physique
  • Etat récurrent

    Formulaire de report


    Etat récurrent \(x\in E\)
    Etat pour lequel le Temps de premier retour est Presque sûrement fini : $${\Bbb P}_x(H_x\lt \infty)=1$$
    • caractérisations :
            
      1. \(N_x\) \(\overset{{\Bbb P}_x-ps}=+\infty\)

        
  • \(U(x,x)=\infty\)
    • un état \(y\) qui n'est pas récurrent est dit transitoire
      •     
    • on a alors en particulier \({\Bbb P}(N_y=k)=\) \(\big(1-{\Bbb P}_y(H_y\lt \infty)\big){\Bbb P}_y(H_y\lt \infty)^{k-1}\) et \({\Bbb E}_y[N_y]=\) \(\frac1{{\Bbb P}_y(H_y=\infty)}\)
      •     
    • on a aussi \(\forall x\in E\), \({\Bbb P}_x(N_y\lt \infty)=1\)
    • on note \(R\) l'ensemble des points récurrents
      •     
    • \(R\) peut être partitionné en classes de récurrence \(R=\bigcup_{i\in I}R_i\) de manière à ce que \(\forall x\in R_i,\forall z\in R_i,\forall y\in E\setminus R_i\), \(N_z\overset{{\Bbb P}_x-ps}=\infty\) et \(N_y\overset{{\Bbb P}_x-ps}=0\)
      •         
    • si \(x\in R\setminus E\), alors soit la Chaîne de Markov reste transitoire, soit elle passe par un état récurrent à un moment et reste indéfiniment dans sa composante \(R_i\)


    Exemples

    Classifier les états de cette chaîne de Markov.

    Le point de départ est donné par \({\Bbb P}_x\).

    La probabilité que le nombre de visites soit infini peut alors être calculé via le Lemme de Borel-Cantelli, en fonction de \(\mu(x)\).

    Finalement, il n'y a qu'une seule classe de récurrence.


    Classifier les états de cette chaîne de Markov :

    Pour deux points donné, il existe un nombre d'étapes tel que la probabilité de joindre ces deux points en ce nombre d'étapes est non nul (par convexité).

    Donc il y a soit \(1\), soit \(0\) classe de récurrence.

    Finalement, la chaîne est récurrente irréductible puisque le nombre d'états est fini.


    Classifier les états de cette chaîne de Markov :

    \(0\) est récurrent car absorbant.

    Il faut ensuite faire une disjonction de cas en fonction de \(\mu(0)\).

    Dans les deux cas, tout entier non nul \(k\) est transitoire, car il mène à \(0\), mais \(0\) ne mène pas à \(k\) \(\to\) tous les entiers non nuls sont transitoires.



    Classifier les états de cette chaîne de Markov :

    Le noyau potentiel entre deux nombres est le même qu'entre leur différence et \(0\).

    En particulier, le noyau potentiel d'un état vers lui-même est le même que celui de \(0\) vers \(0\).

    On en déduit que tous les états sont de même type.

    En fait, leur classification dépend de la moyenne \(m\).


    START
    Ω Basique (+inversé optionnel)
    Recto: Donner un exemple classique de chaîne de Markov avec plusieurs classes de récurrence.
    Verso:

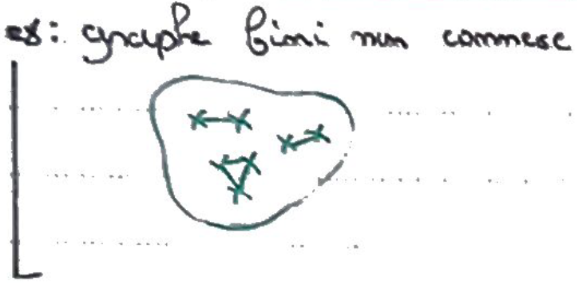
    Bonus:
    Carte inversée ?:
    END
    START
    Ω Basique (+inversé optionnel)
    Recto: Donner un exemple de marche aléatoire sur \({\Bbb Z}\) pour laquelle il y a plusieurs classes de récurrence.
    Verso:

    Bonus:
    Carte inversée ?:
    END
    Faire \(i.\)

    On a une première inégalité en supprimant le \(\max\).

    Le reste vient via un théorème belge et en passant au \(\sup\).


    Faire \(ii.\)

    La Loi forte des grands nombres nous donne la convergence ps des moyennes de \(Y_k\).

    Insérer cette limite dans \(Z\) : c'est un \(\sup\) de suite qui tend vers qqch de négatif.

    On en déduit que le \(\sup\) est atteint par une valeur finie, donc il est fini.


    Faire \(iii.\)

    Utiliser l'inégalité établie précédemment pour réécrire l'événement.

    Lorsque \(x\) devient très grand, cela tend vers une probabilité nulle (puisque \(Z\) est fini ps).


    Faire \(iv.\)

    D'après les étapes précédentes, on peut majorer le temps de premier retour en \(0\) lorsque \(x\) est assez grand.

    On peut alors minorer la probabilité de non-retour en \(0\) via la probabilité de passer par \(x\) (ce qui est facilement minorable) en montrer qu'elle est positive.


  • Rétroliens :
    • Mesure invariante